publications

2024

1. 

   Implications of Data Topology for Deep Generative Models

   Jin Yinzhu, Rory McDaniel, Joseph N. Tatro, Michael J. Catanzaro, Abraham D. Smith, Paul Bendich, Matthew B. Dwyer, and P. Thomas Fletcher

   Frontiers in Computer Science, 2024

   HTML

2. 

   Topological Decompositions Enhance Efficiency of Reinforcement Learning

   Michael J Catanzaro, Aaron Dharna, Jay Hineman, James B Polly, Kevin McGoff, Abraham D Smith, and Paul Bendich

   2024 IEEE Aerospace, 2024

   Abs HTML

   Coordinating multiple sensors can be expressed as a reinforcement learning [RL] problem. Deep RL has excelled at observation processing (for example using convolution networks to process gridded data), but it suffers from sample inefficiency. To address this problem, we topologically decompose the total observation space into overlapping components, using the detection of co-incidence or spatial adjacency of the sensors to construct a stratified decomposition analogous. By allowing the RL agent to learn within the context of this decomposition and take advantage of it through action masking, we achieve positive reward and efficient gains over the learning process. We demonstrate performance and efficiency gains through several experiments using a bespoke game implementation that combines RLlib, Griddly, and Gymnasium. We draw analogies between our games and more general co-incidence in sensing space, time, or modality. We find that our decomposition can be combined with modern RL algorithms to learn high-performing sensor control policies, and our pipeline scales well as the number of sensors grows.

2023

1. 

   Harmonic representatives in homology over arbitrary fields

   Michael J. Catanzaro, and Brantley Vose

   Journal of Applied and Computational Topology, Mar 2023

   Abs arXiv HTML

   We introduce a notion of harmonic chain for chain complexes over fields of positive characteristic. A list of conditions for when a Hodge decomposition theorem holds in this setting is given and we apply this theory to finite CW complexes. An explicit construction of the harmonic chain within a homology class is described when applicable. We show how the coefficients of usual discrete harmonic chains due to Eckmann can be reduced to localizations of the integers, allowing us to compare classical harmonicity with the notion introduced here. We focus on applications throughout, including CW decompositions of orientable surfaces and examples of spaces arising from sampled data sets.

2. 

   Topological Parallax: A Geometric Specification for Deep Perception Models

   Abraham Smith, Michael Catanzaro, Gabrielle Angeloro, Nirav Patel, and Paul Bendich

   In Advances in Neural Information Processing Systems , Mar 2023

   arXiv HTML Code

3. 

   Topological Data Analysis Captures Task-Driven fMRI Profiles in Individual Participants: A Classification Pipeline Based on Persistence

   Michael J. Catanzaro, Sam Rizzo, John Kopchick, Asadur Chowdury, David R Rosenberg, Peter Bubenik, and Vaibhav A Diwadkar

   Neuroinformatics, Nov 2023

   Abs HTML

   BOLD-based fMRI is the most widely used method for studying brain function. The BOLD signal while valuable, is beset with unique vulnerabilities. The most notable of these is the modest signal to noise ratio, and the relatively low temporal and spatial resolution. However, the high dimensional complexity of the BOLD signal also presents unique opportunities for functional discovery. Topological Data Analyses (TDA), a branch of mathematics optimized to search for specific classes of structure within high dimensional data may provide particularly valuable applications. In this investigation, we acquired fMRI data in the anterior cingulate cortex (ACC) using a basic motor control paradigm. Then, for each participant and each of three task conditions, fMRI signals in the ACC were summarized using two methods: a) TDA based methods of persistent homology and persistence landscapes and b) non-TDA based methods using a standard vectorization scheme. Finally, using machine learning (with support vector classifiers), classification accuracy of TDA and non-TDA vectorized data was tested across participants. In each participant, TDA-based classification out-performed the non-TDA based counterpart, suggesting that our TDA analytic pipeline better characterized task- and condition-induced structure in fMRI data in the ACC. Our results emphasize the value of TDA in characterizing task- and condition-induced structure in regional fMRI signals. In addition to providing our analytical tools for other users to emulate, we also discuss the unique role that TDA-based methods can play in the study of individual differences in the structure of functional brain signals in the healthy and the clinical brain.

4. 

   Combinatorial Exploration of Morse–Smale Functions on the Sphere via Interactive Visualization

   Youjia Zhou, Jānis Lazovskis, Michael J. Catanzaro, Matthew Zabka, and Bei Wang

   In 2023 Topological Data Analysis and Visualization (TopoInVis) , Nov 2023

   Abs HTML

   In this paper, we are interested in the characterization and classification of Morse–Smale functions. To that end, we present MSF Designer, an interactive visualization tool that supports the combinatorial exploration of Morse–Smale functions on the sphere. Our tool supports the design and visualization of a Morse–Smale function in a simple way using fundamental moves, which are combinatorial operations introduced by Catanzaro et al. that modify the Morse–Smale graph of the function. It also provides fine-grained control over the geometry and topology of its gradient vector field. The tool is designed to help mathematicians explore the complex configuration spaces of Morse–Smale functions, as well as their associated gradient vector fields and Morse–Smale complexes. Understanding these spaces will help mathematicians expand their applicability in topological data analysis and visualization. In particular, our tool helps topologists, geometers, and combinatorialists explore invariants in the classification of vector fields and characterize Morse functions in the persistent homology setting.

2022

1. 

   Fluctuations of cycles in a finite CW complex

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Israel Journal of Mathematics, Apr 2022

   Abs arXiv HTML

   We use algebraic topology to study the stochastic motion of cellular cycles in a finite CW complex. Inspired by statistical mechanics, we introduce a homological observable called the average current. The latter measures the average flux of the probability in the process. In the low temperature, adiabatic limit, we prove that the average current fractionally quantizes, in which the denominators are combinatorial invariants of the CW complex.

2. 

   Persistence landscapes of affine fractals

   Michael J. Catanzaro, Lee Przybylski , and Eric S. Weber

   Demonstratio Mathematica, May 2022

   Abs arXiv HTML

   We develop a method for calculating the persistence landscapes of affine fractals using the parameters of the corresponding transformations. Given an iterated function system of affine transformations that satisfies a certain compatibility condition, we prove that there exists an affine transformation acting on the space of persistence landscapes, which intertwines the action of the iterated function system. This latter affine transformation is a strict contraction and its unique fixed point is the persistence landscape of the affine fractal. We present several examples of the theory as well as confirm the main results through simulations.

2021

1. Probability measures on graph trajectories

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Submitted, May 2021

   Abs arXiv

   The aim of this note is to construct a probability measure on the space of trajectories in a continuous time Markov chain having a finite state diagram, or more generally which admits a global bound on its degree and rates. Our approach is elementary. Our main intention is to fill a gap in the literature.

2. 

   Multiparameter persistent homology via generalized Morse theory

   Peter Bubenik, and Michael J. Catanzaro

   Toric Topology and Polyhedral Products, Proceedings of the Fields Insitute, Spring Nature Switzerland, Jul 2021

   Abs arXiv HTML

   We define a class of multiparameter persistence modules that arise from a one-parameter family of functions on a topological space. In the case of smooth functions on a compact manifold, we apply cobordism theory and Cerf theory to study the resulting persistence modules. We give examples in which we obtain a complete description of the persistence module as a direct sum of indecomposable summands and provide a corresponding visualization.

3. 

   From mathematics to medicine: A practical primer on topological data analysis (TDA) and the development of related analytic tools for the functional discovery of latent structure in fMRI data

   Andrew Salch, Adam Regalski, Hassan Abdallah, Raviteja Suryadevara, Michael J. Catanzaro, and Vaibhav A. Diwadkar

   PLOS ONE, Aug 2021

   Abs HTML

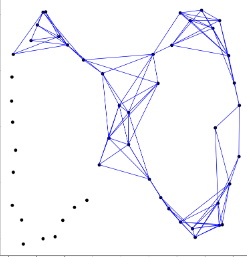
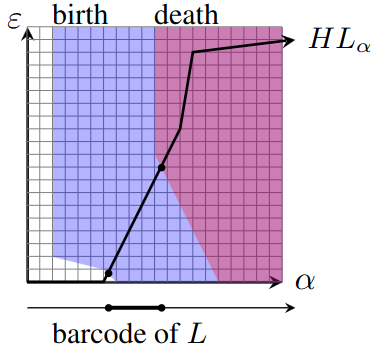
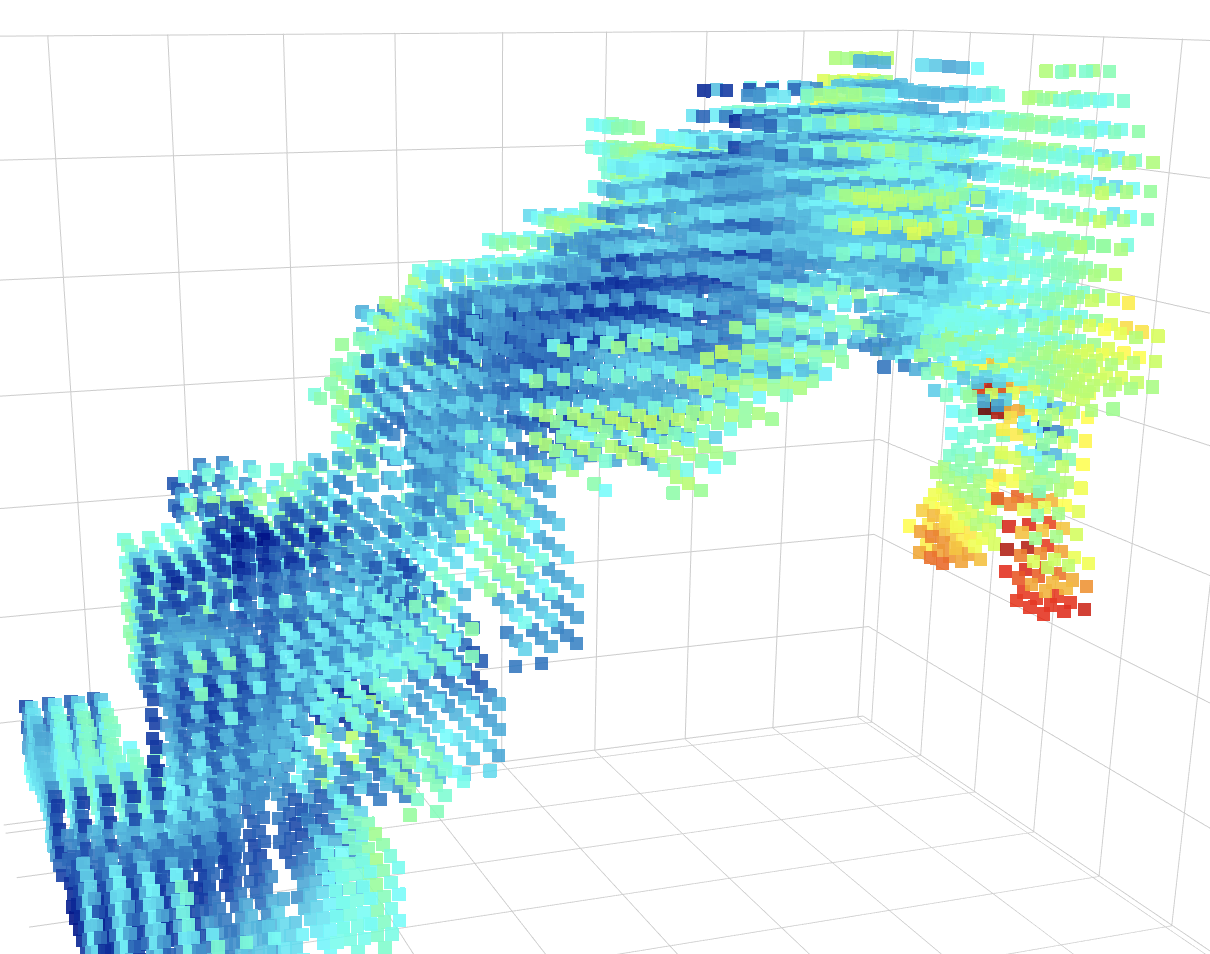
   fMRI is the preeminent method for collecting signals from the human brain in vivo, for using these signals in the service of functional discovery, and relating these discoveries to anatomical structure. Numerous computational and mathematical techniques have been deployed to extract information from the fMRI signal. Yet, the application of Topological Data Analyses (TDA) remain limited to certain sub-areas such as connectomics (that is, with summarized versions of fMRI data). While connectomics is a natural and important area of application of TDA, applications of TDA in the service of extracting structure from the (non-summarized) fMRI data itself are heretofore nonexistent. “Structure” within fMRI data is determined by dynamic fluctuations in spatially distributed signals over time, and TDA is well positioned to help researchers better characterize mass dynamics of the signal by rigorously capturing shape within it. To accurately motivate this idea, we a) survey an established method in TDA (“persistent homology”) to reveal and describe how complex structures can be extracted from data sets generally, and b) describe how persistent homology can be applied specifically to fMRI data. We provide explanations for some of the mathematical underpinnings of TDA (with expository figures), building ideas in the following sequence: a) fMRI researchers can and should use TDA to extract structure from their data; b) this extraction serves an important role in the endeavor of functional discovery, and c) TDA approaches can complement other established approaches toward fMRI analyses (for which we provide examples). We also provide detailed applications of TDA to fMRI data collected using established paradigms, and offer our software pipeline for readers interested in emulating our methods. This working overview is both an inter-disciplinary synthesis of ideas (to draw researchers in TDA and fMRI toward each other) and a detailed description of methods that can motivate collaborative research.

4. 

   A model for random chain complexes

   Michael J. Catanzaro, and Matthew J. Zabka

   Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, Oct 2021

   Abs arXiv HTML

   We introduce a model for random chain complexes over a finite field. The randomness in our complex comes from choosing the entries in the matrices that represent the boundary maps uniformly over q , conditioned on ensuring that the composition of consecutive boundary maps is the zero map. We then investigate the combinatorial and homological properties of this random chain complex.

2020

1. 

   Moduli spaces of morse functions for persistence

   Michael J. Catanzaro, Justin M. Curry, Brittany Terese Fasy, Jānis Lazovskis, Greg Malen, Hans Riess, Bei Wang, and Matthew Zabka

   Journal of Applied and Computational Topology, Sep 2020

   Abs arXiv HTML

   We consider different notions of equivalence for Morse functions on the sphere in the context of persistent homology and introduce new invariants to study these equivalence classes. These new invariants are as simple—but more discerning than—existing topological invariants, such as persistence barcodes and Reeb graphs. We give a method to relate any two Morse–Smale vector fields on the sphere by a sequence of fundamental moves by considering graph-equivalent Morse functions. We also explore the combinatorially rich world of height-equivalent Morse functions, considered as height functions of embedded spheres in R^3. Their level set invariant, a poset generated by nested disks and annuli from level sets, gives insight into the moduli space of Morse functions sharing the same persistence barcode.

2. 

   Hypercurrents

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Submitted, Nov 2020

   Abs arXiv

   We introduce the notion of a protocol, which consists of a space whose points are labeled by real numbers indexed by the set of cells of a fixed CW complex in prescribed degrees, where the labels are required to vary continuously. If the space is a one-dimensional manifold, then a protocol determines a continuous time Markov chain. When a homological gap condition is present, we associate to each protocol a ’characteristic’ cohomology class which we call the hypercurrent. The hypercurrent comes in two flavors: one algebraic topological and the other analytical. For generic protocols we show that the analytical hypercurrent tends to the topological hypercurrent in the low temperature limit. We also exhibit examples of protocols having nontrivial hypercurrent.

2017

1. 

   Exciton scattering via algebraic topology

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Journal of Topology and Analysis, Aug 2017

   Abs arXiv HTML

   This paper introduces an intersection theory problem for maps into a smooth manifold equipped with a stratification. We investigate the problem in the special case when the target is the unitary group U(n)U(n)\textlessmath display="inline" overflow="scroll" altimg="eq-00001.gif"\textgreater\textlessmi\textgreaterU\textless/mi\textgreater\textlessmo class="MathClass-open" stretchy="false"\textgreater(\textless/mo\textgreater\textlessmi\textgreatern\textless/mi\textgreater\textlessmo class="MathClass-close" stretchy="false"\textgreater)\textless/mo\textgreater\textless/math\textgreater and the domain is a circle. The first main result is an index theorem that equates a global intersection index with a finite sum of locally defined intersection indices. The local indices are integers arising from the geometry of the stratification. The result is used to study a well-known problem in chemical physics, namely, the problem of enumerating the electronic excitations (excitons) of a molecule equipped with scattering data.

2. 

   A higher Boltzmann distribution

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Journal of Applied and Computational Topology, Dec 2017

   Abs arXiv HTML

   We characterize the classical Boltzmann distribution as the unique solution to a combinatorial Hodge theory problem in homological degree zero on a finite graph. By substituting for the graph a CW complex X and a choice of degree d≤dimXd≤dim⁡Xd }le }dim X, we define by direct analogy a higher dimensional Boltzmann distribution ρBρB}rho ^B as a certain real-valued cellular (d−1)(d−1)(d-1)-cycle. We then give an explicit formula for ρBρB}rho ^B. We explain how these ideas relate to the Higher Kirchhoff Network Theorem of Catanzaro et al. (Homol Homotopy Appl 17:165–189, 2015). We also deduce an improved version of the Higher Matrix-Tree Theorems of Catanzaro et al. (Homol Homotopy Appl 17:165–189, 2015).

2016

1. 

   Stochastic dynamics of extended objects in driven systems II: Current quantization in the low-temperature limit

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Chemical Physics, Dec 2016

   Abs HTML

   Driven Langevin processes have appeared in a variety of fields due to the relevance of natural phenomena having both deterministic and stochastic effects. The stochastic currents and fluxes in these systems provide a convenient set of observables to describe their non-equilibrium steady states. Here we consider stochastic motion of a ( k - 1 ) -dimensional object, which sweeps out a k-dimensional trajectory, and gives rise to a higher k-dimensional current. By employing the low-temperature (low-noise) limit, we reduce the problem to a discrete Markov chain model on a CW complex, a topological construction which generalizes the notion of a graph. This reduction allows the mean fluxes and currents of the process to be expressed in terms of solutions to the discrete Supersymmetric Fokker–Planck (SFP) equation. Taking the adiabatic limit, we show that generic driving leads to rational quantization of the generated higher dimensional current. The latter is achieved by implementing the recently developed tools, coined the higher-dimensional Kirchhoff tree and co-tree theorems. This extends the study of motion of extended objects in the continuous setting performed in the prequel (Catanzaro et al.) to this manuscript.

2. 

   Stochastic dynamics of extended objects in driven systems: I. Higher-dimensional currents in the continuous setting

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Chemical Physics, Dec 2016

   Abs HTML

   The probability distributions, as well as the mean values of stochastic currents and fluxes, associated with a driven Langevin process, provide a good and topologically protected measure of how far a stochastic system is driven out of equilibrium. By viewing a Langevin process on a compact oriented manifold of arbitrary dimension m as a theory of a random vector field associated with the environment, we are able to consider stochastic motion of higher-dimensional objects, which allow new observables, called higher-dimensional currents, to be introduced. These higher dimensional currents arise by counting intersections of a k -dimensional trajectory, produced by a evolving ( k - 1 ) -dimensional cycle, with a reference cross section, represented by a cycle of complimentary dimension ( m - k ) . We further express the mean fluxes in terms of the solutions of the Supersymmetric Fokker–Planck (SFP), thus generalizing the corresponding well-known expressions for the conventional currents.

3. 

   A Topological Study Of Stochastic Dynamics On CW Complexes

   Michael Catanzaro

   Wayne State University Dissertations, Jan 2016

   Abs HTML

   In this dissertation, we consider stochastic motion of subcomplexes of a CW complex, and explore the implications on the underlying space. The random process on the complex is motivated from Ito diffusions on smooth manifolds and Langevin processes in physics. We associate a Kolmogorov equation to this process, whose solutions can be interpretted in terms of generalizations of electrical, as well as stochastic, current to higher dimensions. These currents also serve a key function in relating the random process to the topology of the complex. We show the average current generated by such a process can be written in a physically familiar form, consisting of the solution to Kirchhoff’s network problem and the Boltzmann distribution, suitably generalized to arbitrary dimensions. We analyze these two components in detail, and discover they reveal an unexpected amount of information about the topology of the CW complex. The main result is a quantization result for the average current in the low temperature, adiabatic limit. As an application, we express the Reidemeister torsion of the complex, a topological invariant, in terms of these quantities.

4. 

   A user’s guide: Dynamics and fluctuations of cellular cycles on CW complexes

   Michael J Catanzaro

   Enchiridion: Mathematics User’s Guides, Jan 2016

   HTML

2015

1. 

   Kirchhoff’s theorems in higher dimensions and Reidemeister torsion

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Homology, Homotopy and Applications, Jan 2015

   HTML

2. 

   Counting the number of excited states in organic semiconductor systems using topology

   Michael J. Catanzaro, Tian Shi, Sergei Tretiak, and Vladimir Y. Chernyak

   The Journal of Chemical Physics, Feb 2015

   Abs arXiv HTML

   Exciton scattering theory attributes excited electronic states to standing waves in quasi-one-dimensional molecular materials by assuming a quasi-particle picture of optical excitations. The quasi-particle properties at branching centers are described by the corresponding scattering matrices. Here, we identify the topological invariant of a scattering center, referred to as its winding number, and apply topological intersection theory to count the number of quantum states in a quasi-one-dimensional system.

2014

1. 

   Excited-State Structure Modifications Due to Molecular Substituents and Exciton Scattering in Conjugated Molecules

   Hao Li, Michael J. Catanzaro, Sergei Tretiak, and Vladimir Y. Chernyak

   The Journal of Physical Chemistry Letters, Feb 2014

   Abs HTML

   Attachment of chemical substituents (such as polar moieties) constitutes an efficient and convenient way to modify physical and chemical properties of conjugated polymers and oligomers. Associated modifications in the molecular electronic states can be comprehensively described by examining scattering of excitons in the polymer?s backbone at the scattering center representing the chemical substituent. Here, we implement effective tight-binding models as a tool to examine the analytical properties of the exciton scattering matrices in semi-infinite polymer chains with substitutions. We demonstrate that chemical interactions between the substitution and attached polymer are adequately described by the analytical properties of the scattering matrices. In particular, resonant and bound electronic excitations are expressed via the positions of zeros and poles of the scattering amplitude, analytically continued to complex values of exciton quasi-momenta. We exemplify the formulated concepts by analyzing excited states in conjugated phenylacetylenes substituted by perylene.

2013

1. 

   On Kirchhoff’s theorems with coefficients in a line bundle

   Michael J. Catanzaro, Vladimir Y. Chernyak, and John R. Klein

   Homology, Homotopy and Applications, Dec 2013

   Abs arXiv HTML

   We prove “twisted” versions of Kirchhoff’s network theorem and Kirchhoff’s matrix-tree theorem on connected finite graphs. Twisting here refers to chains with coefficients in a flat unitary line bundle.

2011

1. 

   Generalized Tonnetze

   Michael J. Catanzaro

   Journal of Mathematics and Music, Dec 2011

   Abs arXiv HTML

   We study a generalization of the classical Riemannian Tonnetz to N-tone equally tempered scales (for all N) and arbitrary triads. We classify all the spaces that result. The torus turns out to be the most common possibility, especially as N grows. Other spaces include 2-simplices, tetrahedra boundaries, and the harmonic strip (in both its cylinder and Mobius band variants). The final and most exotic space we find is something we call a ‘circle of tetrahedra boundaries’. These are the Tonnetze for spaces of triads which contain a tritone. They are closely related to Peck’s Klein bottle Tonnetz.

2. 

   Finitely Presented Graded Modules over the Steenrod Algebra in Sage

   Michael J Catanzaro

   Dec 2011

   HTML Code