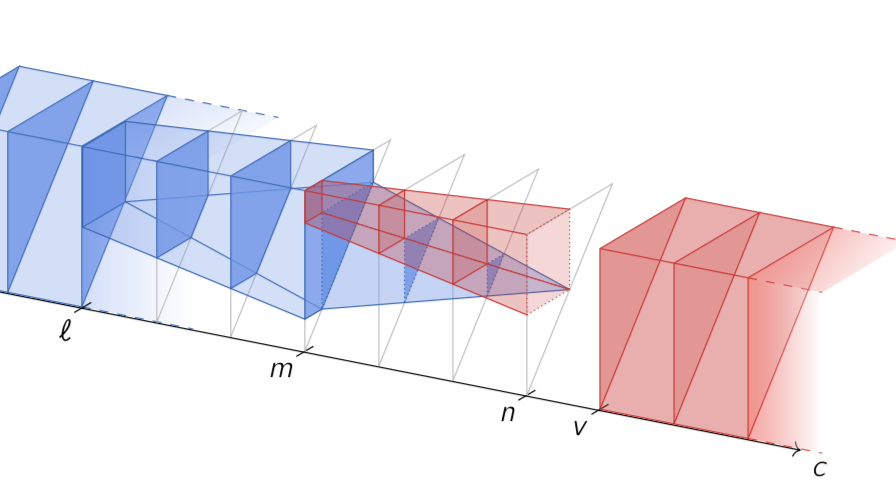
As a postdoc, I began work on geometric models for studying multiparameter persistence. One of the first examples of ordinary persistence arose from studying the sub-level sets of a Morse function. Together with Peter Bubenik, we propose looking at generic families of Morse functions to study multiparameter persistent homology in (Bubenik & Catanzaro, 2021). Using tools from geometric topology, we attempt to build a decomposition of the associated multiparameter persistence module, analogous to the barcode.
References
2021
-
Multiparameter persistent homology via generalized Morse theory
Toric Topology and Polyhedral Products, Proceedings of the Fields Insitute, Spring Nature Switzerland, Jul 2021
We define a class of multiparameter persistence modules that arise from a one-parameter family of functions on a topological space. In the case of smooth functions on a compact manifold, we apply cobordism theory and Cerf theory to study the resulting persistence modules. We give examples in which we obtain a complete description of the persistence module as a direct sum of indecomposable summands and provide a corresponding visualization.