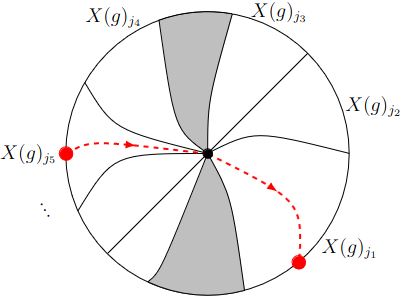
Exciton Scattering
Excitons are naturally occurring quasi-particles associated with the conversion of light to energy (e.g. photosynthesis). Our work applies algebraic topology to study and in particular, to count the number of such excitations in certain systems. We formulate this problem as a non-standard intersection theory problem of stratified spaces. In particular, we study intersections of a smooth curve with a stratified non-manifold inside the unitary group. Each intersection is weighted with a multiplicity, and the number of excitons can be computed via a topological winding number with an index-like theorem.
The mathematical intersection theory is developed in (Catanzaro et al., 2017). We focus on the intersection of a curve with the subspace of matrices with at least one eienvalue equal to one inside the manifold of all \(n \times n\) unitary matrices.
The code is simple. Just wrap your images with <div class="col-sm"> and place them inside <div class="row"> (read more about the Bootstrap Grid system). To make images responsive, add img-fluid class to each; for rounded corners and shadows use rounded and z-depth-1 classes. Here’s the code for the last row of images above: